Точки А и В лежат по сторону от прямой. Из этих точек к данной прямой проведены...

Question

Точки А и В лежат по сторону от прямой. Из этих точек к данной прямой проведены перпендикуляры АМ и ВN так , что АМ=ВN и угол NAM =углу MBN.
Докажите ,что угол ANM =углу BMN. И пожалуйста сделайте фото рисунка,ибо я не понял как его изобразить (ну или объясните как его начертить,ну или попытайтесь с помощью символов изобразить) 25 б !!!!

Comments

Оооо Спасиибо!!!! 3 раза писал эту задачу сюда

---

Да она вообще элементарная, щас...

---

Жду... )

---

Ты издеваешься?

---

Рисунок в пейнте небыстро рисовать...

---

Если ты такой резвый, что ж сам тогда не решаешь?.. )))

---

там не лишнее "угол NAM =углу MBN" и я геометрию не понимаю

---

а так нельзя? решение: рассмотрим треугольники АМВ и ВNM. Известно, что угол AMN=BNM=90градусов. И углы NAM и MBN равны т.к у них общая сторона MN и AM=BN. Следовательно треугольники подобны т.к. у них равны 2 угла, а значит равен и третий( третий угол это ANM и BMN)

---

Там как угодно можно. Можно так: AMN=BNM=90градусов, углы NAM и MBN равны, AM=BN, значит треуг. равны по второму признаку. Только в этой задаче именно "РАВНЫ", а не подобны...

---

Спасибо

Answer 1

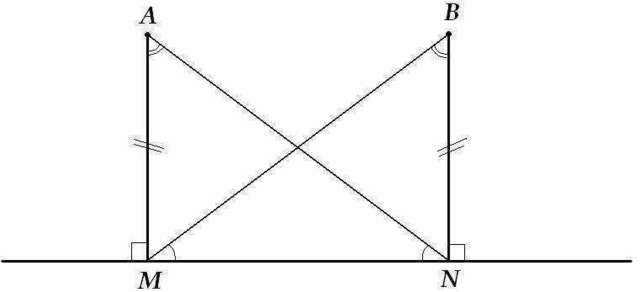
ΔAMN и ΔBNM - прямоугольные, AM=BN, MN - общая сторона, значит  ΔAMN=ΔBNM по первому признаку равенства треугольников (или по второму признаку равенства прямоугольных треугольников), значит ∠ANM=∠BMN
В условии ∠NAM =∠MBN - совершенно лишнее, и без этого решается.

---