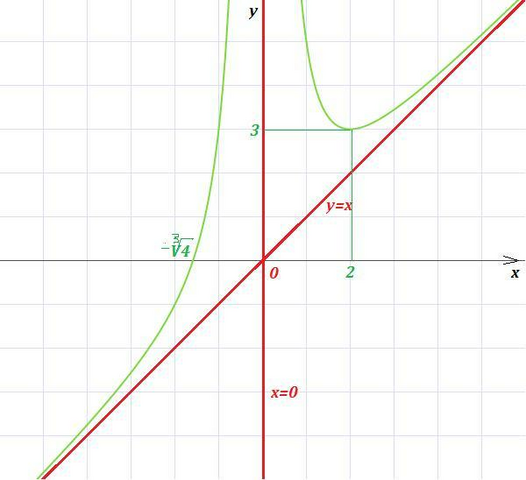
Функция общего вида ( не явл. ни чётной, ни нечётной).
![3)\; \; \lim\limits _{x \to 0}\Big (x+\frac{4}{x^2}\Big )=0+\infty =\infty \; \; \Rightarrow \; \; x=0\; -\; vertikalnaya\; asimptota\\\\\lim\limits _{x \to \infty}\frac{x^3+4}{x^2}=\infty \\\\y=kx+b\\\\k=\lim\limits _{x \to \infty}\frac{y(x)}{x}=\lim\limits _{x \to \infty}\frac{x^3+4}{x^2\cdot x}=1\\\\b=\lim\limits _{x \to \infty}(y(x)-kx)=\lim\limits _{x \to \infty}(\frac{x^3+4}{x^2}-x)=\lim\limits _{x \to \infty}\frac{4}{x^2}=0\\\\y=x\; -\; naklonnaya\; asimptota\\\\4)\; \; \frac{x^3+4}{x^2}=0\; \; \to\; \; x^3+4=0\; ,\; \; x=-\sqrt[3]{4}](https://tex.z-dn.net/?f=3%29%5C%3B%20%5C%3B%20%5Clim%5Climits%20_%7Bx%20%5Cto%200%7D%5CBig%20%28x%2B%5Cfrac%7B4%7D%7Bx%5E2%7D%5CBig%20%29%3D0%2B%5Cinfty%20%3D%5Cinfty%20%5C%3B%20%5C%3B%20%5CRightarrow%20%5C%3B%20%5C%3B%20x%3D0%5C%3B%20-%5C%3B%20vertikalnaya%5C%3B%20asimptota%5C%5C%5C%5C%5Clim%5Climits%20_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7Bx%5E3%2B4%7D%7Bx%5E2%7D%3D%5Cinfty%20%5C%5C%5C%5Cy%3Dkx%2Bb%5C%5C%5C%5Ck%3D%5Clim%5Climits%20_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7By%28x%29%7D%7Bx%7D%3D%5Clim%5Climits%20_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7Bx%5E3%2B4%7D%7Bx%5E2%5Ccdot%20x%7D%3D1%5C%5C%5C%5Cb%3D%5Clim%5Climits%20_%7Bx%20%5Cto%20%5Cinfty%7D%28y%28x%29-kx%29%3D%5Clim%5Climits%20_%7Bx%20%5Cto%20%5Cinfty%7D%28%5Cfrac%7Bx%5E3%2B4%7D%7Bx%5E2%7D-x%29%3D%5Clim%5Climits%20_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7B4%7D%7Bx%5E2%7D%3D0%5C%5C%5C%5Cy%3Dx%5C%3B%20-%5C%3B%20naklonnaya%5C%3B%20asimptota%5C%5C%5C%5C4%29%5C%3B%20%5C%3B%20%5Cfrac%7Bx%5E3%2B4%7D%7Bx%5E2%7D%3D0%5C%3B%20%5C%3B%20%5Cto%5C%3B%20%5C%3B%20x%5E3%2B4%3D0%5C%3B%20%2C%5C%3B%20%5C%3B%20x%3D-%5Csqrt%5B3%5D%7B4%7D "3)\; \; \lim\limits _{x \to 0}\Big (x+\frac{4}{x^2}\Big )=0+\infty =\infty \; \; \Rightarrow \; \; x=0\; -\; vertikalnaya\; asimptota\\\\\lim\limits _{x \to \infty}\frac{x^3+4}{x^2}=\infty \\\\y=kx+b\\\\k=\lim\limits _{x \to \infty}\frac{y(x)}{x}=\lim\limits _{x \to \infty}\frac{x^3+4}{x^2\cdot x}=1\\\\b=\lim\limits _{x \to \infty}(y(x)-kx)=\lim\limits _{x \to \infty}(\frac{x^3+4}{x^2}-x)=\lim\limits _{x \to \infty}\frac{4}{x^2}=0\\\\y=x\; -\; naklonnaya\; asimptota\\\\4)\; \; \frac{x^3+4}{x^2}=0\; \; \to\; \; x^3+4=0\; ,\; \; x=-\sqrt[3]{4}")
0\; \; pri\; \; x\in ODZ\; (x\ne 0\; )\; \; \to \\\\y(x)\; vognyta\; \; pri\; \; x\in ODZ" alt="x^3=8\; ,\; \; x=\sqrt[3]8=2\; \; ,\; \; x\ne 0\\\\znaki\; y'(x):\; \; +++(0)---[\, 2\, ]+++\\\\.\qquad \qquad \qquad \; \; \nearrow \; \; (0)\; \; \; \; \searrow \; \; [\, 2\, ]\; \; \; \nearrow \\\\6)\; \; x_{min}=2\; \; ,\; \; y_{min}=y(2)=3\\\\7)\; \; y''=(1-\frac{8}{x^3})'=\frac{8\cdot 3x^2}{x^6}=\frac{24}{x^4}>0\; \; pri\; \; x\in ODZ\; (x\ne 0\; )\; \; \to \\\\y(x)\; vognyta\; \; pri\; \; x\in ODZ" align="absmiddle" class="latex-formula">
