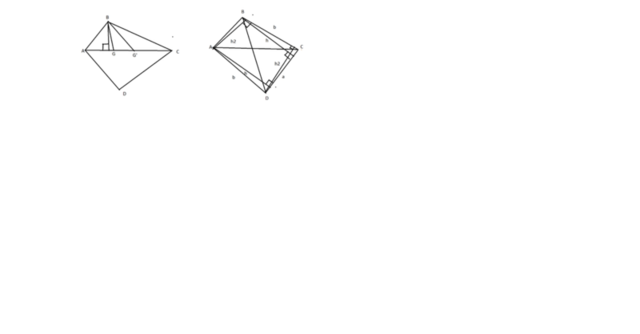
Cмотрим на рисунок слева:
Разрежем 4 угольник как показано на рисунке а именно:
Проведем диагональ AC на ней отмечаем точку G. Проводим GB.
Итак вышло 3 треугольника: ABG BGC ADC (так мы их и разрежем)
ПО условию площадь хотя бы одного треугольника равна 1.
Предположим что площадь либо одного из треугольников
ABG и BGC либо их обоих равна 1. А площадь ADC не равна 1.
Тогда проведем еще 1 отрезок BG'.
Так что BG не равен G'C то естественно площади обоих треугольников изменились при смещении точки G (тк изменились длинны оснований,а высота у всех этих треугольников общая)
Но тогда площади обоих треугольников ABG' и BG'C уже не равны 1.
Но тогда тк из условия хотя бы 1 из площадей равен 1. То площадь ADC равна 1,но это противоречит условию тк при первом разрезании его площадь не была 1.(а треугольник ADC тот же) То мы пришли к противоречию. То раз только среди треугольников ABG BGC не может быть равного 1 площади. То площадь треугольника ADC равна 1.
Анологично в силу симетрии задачи можно доказать что площади всех треугольников: ABC, BCD, ADC ,ABD- равны 1
Посмотрим на 2 рисунок:
У пары треугольников (ADC,BСD) и (ABC ,DBC)
Проведем в каждой паре треугольников высоты на стороны соответственно DC и BC .
Тк треугольники в каждой паре равновеликие (тк все равны 1),а площадь треугольника 1/2осн*высоту. То раз они имеют общие основания. То высоты в каждой паре равны. А тк понятно что если AL и A'L' 2 равных перпендикуляра к прямой Ф.
То прямые Ф и AA' паралельны.
То без ограничений общности выходит что: AB паралельно DC
AD параллельно BC. То есть это параллелограмм.
Тк SADC=SABC=1 то площадь параллелограмма равна 2
Что и требовалось доказать.